Lane-Following with Simple ICRL

A real-world implementation of simple constraint inference for autonomous driving

Simple Constraint Inference for Lane-Following

Reinforcement learning often struggles with complex tasks like autonomous driving, in part due to the difficulty of designing reward functions which properly balance objectives and constraints. A common solution is imitation learning, where the agent is trained in a supervised manner to simply mimic expert behavior. However, imitation learning can be brittle and is prone to compounding errors. A potentially more robust solution lies in IRL, which combines offline expert trajectories with real-world rollouts to learn a reward function. Traditional IRL methods, however, are challenging to train due to their reliance on bi-level adversarial objectives. Does an intermediate solution exist?

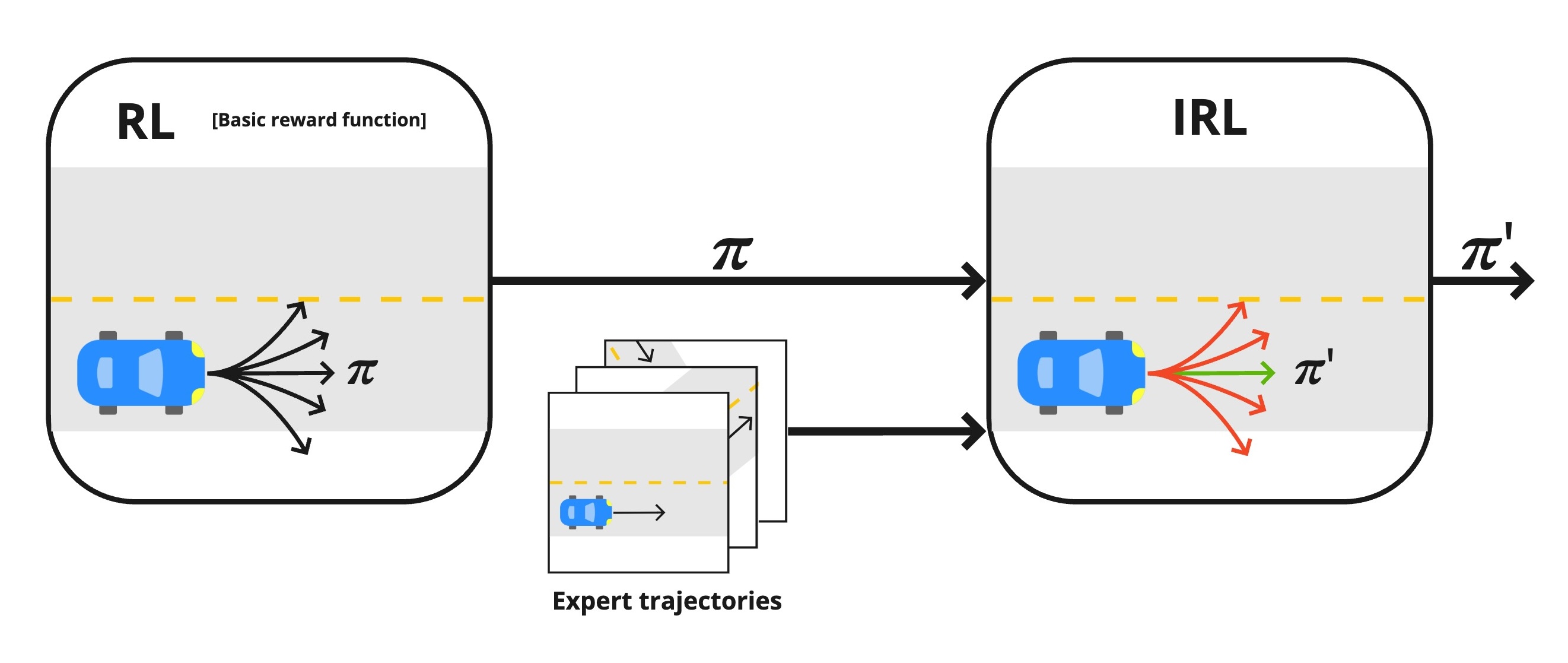
Schematic overview of inverse RL for lane-following constraints

In fact, in many real-world scenarios, there may exist some simple to define primary goal. For example, in autonomous driving, we can define this goal as driving speed or time-to-destination. This goal alone, however, does not explain the expert behavior, which must additionally obey the rules or “constraints” of the road. In this setting, we can consider the potentially easier inverse task of inferring constraints under a known reward function. Precisely, this is the domain of inverse constrained reinforcement learning (ICRL). In their seminal paper on inverse constraint learning, Malik et al , propose an algorithm for inferring constraints from expert data which involves solving a constrained MDP in the inner loop of a maximum-entropy IRL algorithm. This introduces a tri-level optimization, however, which may in fact be more complex to solve than the original IRL problem. In our NeurIPS 2024 paper , we propose a simple reduction of the ICRL problem to an IRL problem, which is equivalent under a broad class of constraint functions, and propose some simple-to-implement practical modifications for the constraint inference case. We show that this can perform as well or better than ICRL methods that explicitly solve a constrained MDP on simulated MuJoCo environments . But does it work in the real world?

In this blog post, we will try it out on an autonomous driving task in the Duckietown environment.

Background

As shown in prior work , the inverse RL problem can be cast as a two-player zero-sum game \begin{equation} \newcommand{\expectation}{\mathbb{E}} \min_{\pi \in \Pi} \sup_{f \in \mathcal{F}} J(\pi_{E},f) - J(\pi, f) \end{equation} where \(\mathcal{F}\) is convex and compact and \(J(\pi, f) = \expectation_{\pi} \left[\sum_{t=0}^T f(s_t,a_t)\right]\).

Similarly, the constrained RL problem with a single constraint can also be cast as a two-player zero-sum game \begin{equation} \min_{\pi \in \Pi}\max_{\lambda \ge 0} -J(\pi, r) + \lambda (J(\pi,c) - \delta). \end{equation}

Finally, show that for inverse constrained RL, these two games can be combined into a three-player game of the following form (where \(r\) is a given reward function in a class \(\mathcal{F}_r\))

\begin{equation} \sup_{c \in \mathcal{F_c}}\max_{\lambda > 0} \min_{\pi \in \Pi} J(\pi_{E},r - \lambda c) - J(\pi, r - \lambda c) \label{eq:tri} \end{equation}

Practically speaking, solving this game involves running IRL where the inner loop optimization solves a constrained MDP using a Lagrangian version of RL.

Method

In our paper , we demonstrate that Equation \ref{eq:tri} can be reduced to a bi-level optimization, equivalent to performing IRL on a reward “correction” term.

\begin{equation}\label{eq:icrl-bilevel} \max_{c\in\mathcal{F_c}}\min_{\pi\in\Pi} J(\pi_E, r - c) - J(\pi, r - c). \end{equation}

where \(r\) is the known reward and \(c\) is the learned constraint. This simplification holds as long as the constraint class \(\mathcal{F_c}\) is closed under scalar positive multiplication.

Practically speaking, this can be implemented by adapting any adversarial IRL algorithm such that the policy learner in the inner loop receives the true reward from the environment adjusted additively by the learnt correction term. The main adjustment from IRL is that the constraint class must be closed to positive scalar multiplication, which excludes passing the neural network output through a bounded output function like sigmoid, as employed in previous ICRL methods . We instead use a linear activation function clipped to the positive range. We propose using soft clipping with a leaky ReLU activation to reduce issues with disappearing gradients and adding an L2 regularizer on the expected cost of the expert trajectories in the discriminator loss in order to prevent the cost function values from exploding. Hence, the discriminator loss becomes:

\begin{equation} \mathcal{L}(\pi, c) = J(\pi_E, r-c) - J(\pi, r-c) + \expectation_{s,a \sim \tau_E}{\left[c(s,a)^2\right]}, \end{equation}

For more details, including additional possible modifications (not used in these experiments) for adapting IRL to ICRL, please see our paper .

Implementation Details for Lane-Following

In the autonomous driving experiments, we employ the method described above along with the following specific implementation details. All of our code and instructions for reproducing the experiments are available in our github.

Environment

All experiments are conducted within the Duckietown ecosystem, a robotics learning environment for autonomous driving. In our simplified setting for autonomous driving, we consider the single constraint of lane following, which means that the driver is required to stay in the right-hand lane at all times and incurs a cost penalty when outside the lane.

• Real-world environment: The real-world setup consists of the Duckiebot and Duckietown. The Duckiebot is a small mobile robot powered by differential drive. It is equipped with a front-facing camera and onboard NVIDIA Jetson Nano. Duckietown is a configurable track consisting of road tiles (straight, curved, intersections) and other elements that can be configured into different topologies. In our experiments, we use a small loop. For more details on the environment, see here.
• Simulated Environment: Gym-Duckietown is a simulation platform with a Gym interface built to simulate the dynamics of the Duckietown ecosystem.

Expert Trajectories:

Expert trajectories are generated by a pure pursuit policy , an implementation for which is provided in the Duckietown simulator. The pure pursuit policy selects a heading angle for the robot based on a circle that is tangent to the current heading and intersects with the robot’s current position and a lookahead point at some distance $L$ on the center curve of the lane. It uses priviledged information available in the simulator, namely the global coordinates of the robot and the lanes of the road.

Algorithm

• RL algorithm: As the policy optimizer, we use DrQ-v2 , an RL-method developed for continuous control in image-based environments. DrQ-v2 is an extension of the Deep Deterministic Policy Gradient (DDPG) algorithm which adds data augmentation to images sampled from the replay buffer. DDPG is an off-policy actor-critic method that jointly learns a Q-function critic network \(Q_{\theta}\) and a deterministic policy network \(\pi_{\phi}\). In DrQ-v2, a CNN-encoder is used to pre-process the images which are then passed to separate actor and critic heads (gradients are not passed through to the encoder from the actor). In our implementation, we also re-use this encoder with a stop-gradient to pre-process the observations sent to the learned constraint function
• Observation and action space: We use a stack of three camera frames of size 84x84 as the observation, so that the final observation is 9x84x84 (three frames each with three RGB channels). The action space is normalized wheel velocities for the left and right wheels. The maximum speed is a fixed parameter.
• Reward function: We use a simple reward function of forward velocity as the primary reward. This simply rewards the agent for moving forward. Additionally, the episode ends in the simulator when the agent drives off the drivable areas, so that the agent is incentivized to stay on the road in order to maximize episode returns.
• Sim2Real: The policy is trained entirely within the simulator and then transferred to the real-world robot. To deploy on the real Duckiebot, we simply take the weights of the actor and encoder networks from the trained policy - no additional fine-tuning is performed except adjusting the maximum velocity. Since the images in the simulator are uncorrupted by any camera distortions, we apply image rectification to the images obtained from the Duckiebot camera. We also resize and stack the images to achieve the final observation of 9x84x84. In the real-world experiments, inference is performed on a laptop and actions are then transmitted to the robot over the network (no onboard computation in performed). In these experiments, we do not perform any specific Sim2Real methods such as domain randomization, though this would be an interesting avenue for future work.

Baselines

We consider three baselines as comparison to our method

• RL with human-designed reward: Our first baseline is an RL-policy trained using a human-designed reward. Notably, since one of the primary advantages of IRL is the reduction in human-effort needed to define good reward functions, our goal is not to compare necessarily to the best-possible human-designed reward, but rather a simple reward that could be devised without significant human effort. Hence, we do not use the best-designed reward functions, such as those used in previous work for lane-following with RL , which do produce good policies with RL alone but required significant engineering. Rather, we select the default reward function provided in the Duckietown simulator. While this reward function is known not to be optimal, this provides a good baseline for what a minimally-engineered reward function could produce.
• RL with velocity reward: The next baseline trains an RL policy on the simple primary goal reward of forward velocity. Hence, this baseline provides an estimate of performance if no IRL fine-tuning to the expert trajectories is performed. Under this reward function, the agent has no incentive to stay within the right lane.
• Full IRL: The final baseline trains IRL from scratch, without access to the simple forward velocity reward function. This baseline provides an estimate for the advantage gained by using a simple reward function as the primary goal, and learning only the remaining “correction” or constraint through IRL.

Results

Simulation

We train our policy and three baselines in simulation for 4M environment steps across three seeds. We then run evaluation for 50 episodes and average the results across the episodes. Error bars are reported as standard error on this average, across the three seeds. We evaluate the performance of the policy according to three metrics (1) deviation heading: the deviation of the robots heading angle from the tangent to the center line (2) distance traveled: the total cumulative distance traveled in the episode and (3) time in lane: the percent of the time the agent spends in the correct (right) lane.

We consider two training regimes (1) training on a single map (a small loop) and (2) training on a mixture of map topologies (two small loops and one large loop). In (1) we evaluate on the same small loop used in training and in (2) we evaluate on the large loop used in training.

Small Loop

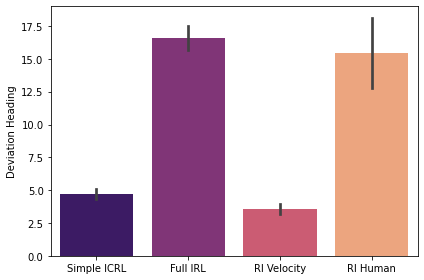
Figure 1: Deviation Heading ↓

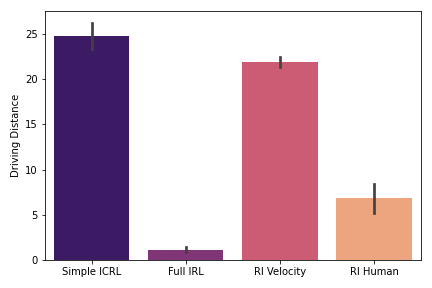
Figure 2: Distance Traveled ↑

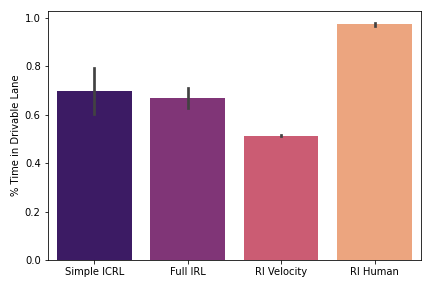
Figure 3: % Time in Lane ↑

Large Loop

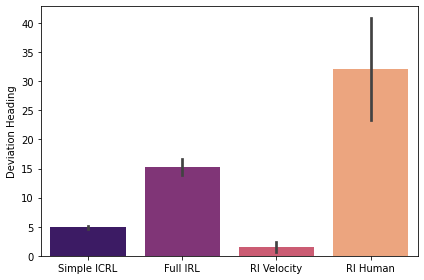
Figure 4: Deviation Heading ↓

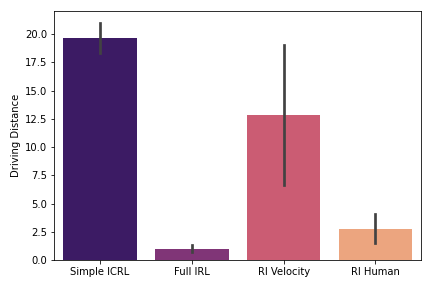
Figure 5: Distance Traveled ↑

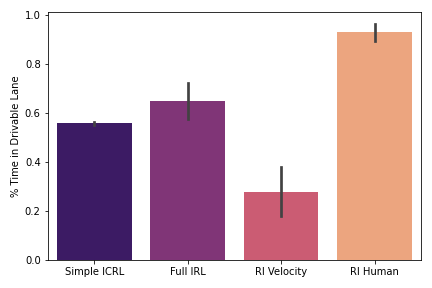
Figure 6: % Time in Lane ↑

A similar pattern of results emerges in both the small and large loops. The RL policy trained on human-designed rewards and the IRL policy trained from scratch mostly fail to learn a useful driving policy, as demonstrated by the low distance traveled (Figures 2 and 5) and the high deviation heading (Figures 1 and 4). Though both policies are relatively strong at staying in the correct lane (Figures 3 and 6), particularly the RL trained on human-designed rewards, the constraint of staying in the lane appears to be too strict, effectively outweighing the primary goal of driving forward.

On the other hand, the policies trained with the velocity reward (Simple ICRL and RL Velocity) successfully learn to drive forward and remain on the road, as demonstrated by the high distance traveled (Figures 2 and 5) and low deviation heading (Figures 1 and 4). However, this comes at the expense of constraint violations, with both policies spending more time outside the lane (Figures 3 and 6). Importantly, however, the Simple ICRL policy, which uses IRL to learn the lane following constraint, provides a significant improvement over the RL Velocity policy in terms of time spent in lane. This is particularly evident in the large loop, in which the Simple ICRL policy nearly doubles the time spent in lane versus the RL Velocity policy.

To further illustrate the difference between the policies, we examine example videos of trajectories from each policy.

Small Loop

Full IRL

RL Human

Simple ICRL

RL Velocity

Large Loop

Full IRL

RL Human

Simple ICRL

RL Velocity

As expected, the videos of the Full IRL and RL Human policies stay in the lane but at the expense of making any significant forward progress, which is consistent with the metrics reported in the Figures above. If we compare the videos from Simple ICRL and RL Velocity in the small loop, we can see that both perform well at driving forward, but Simple ICRL stays in the right lane whereas RL Velocity changes lanes at the beginning of the simulation, consistent with the higher percent time spent in the lane shown in Figure 3.

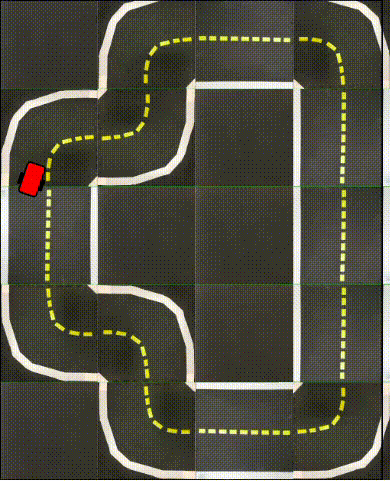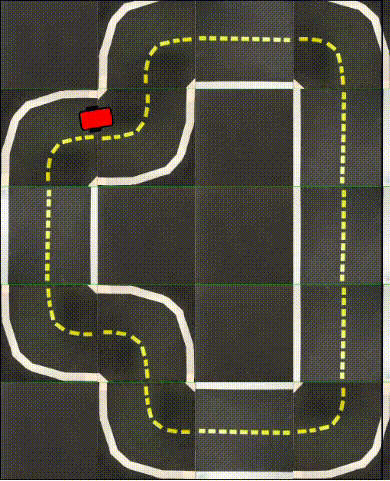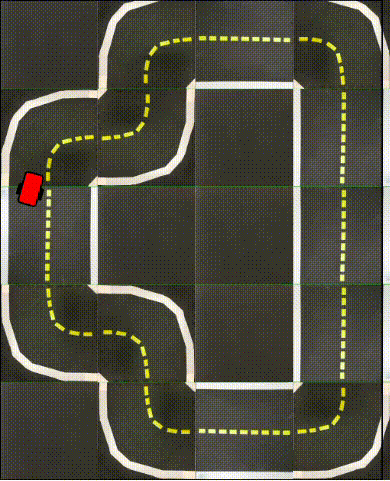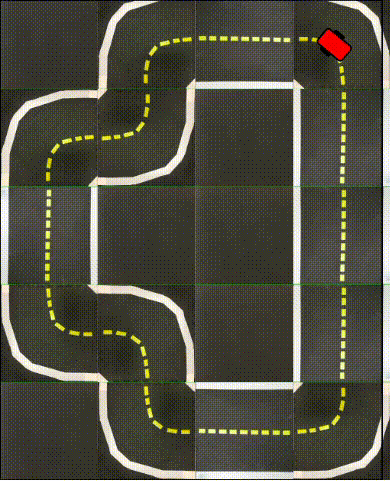
Finally, in the following videos, we show top-down examples of full trajectories of Simple ICRL in simulation.

Small Loop

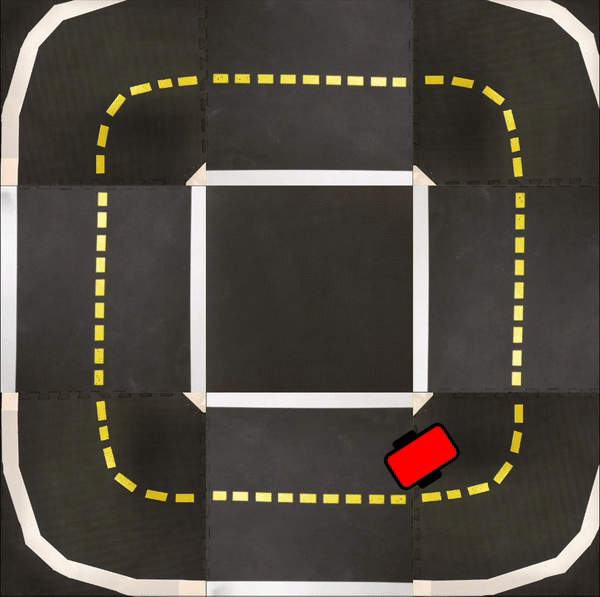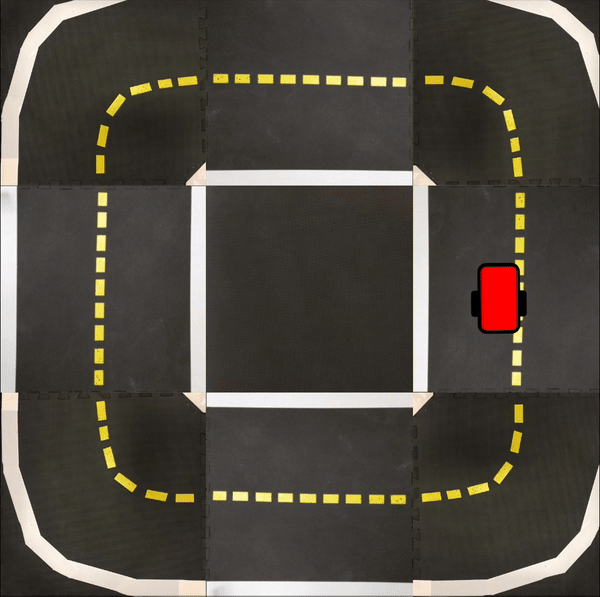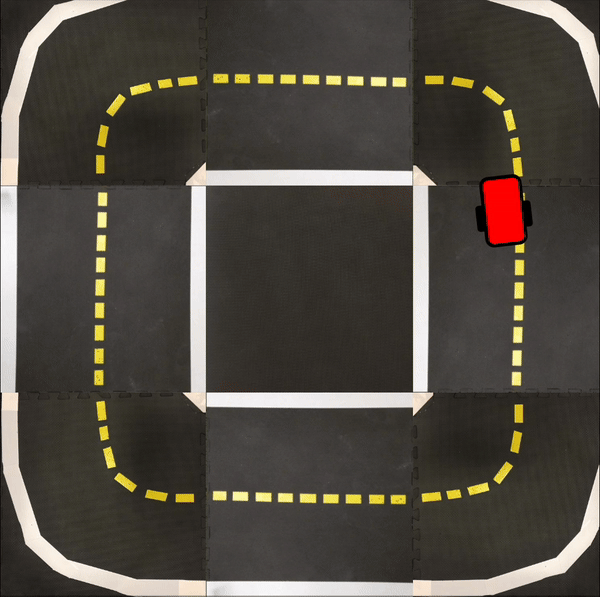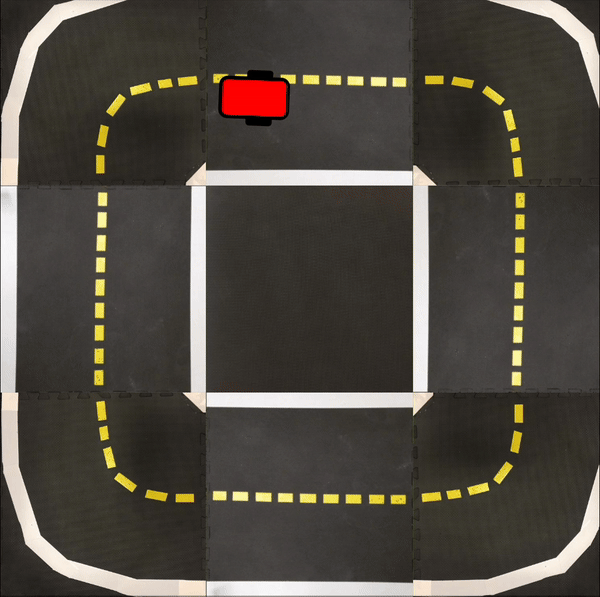
Large Loop

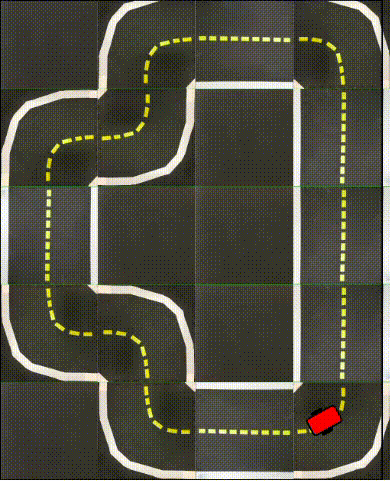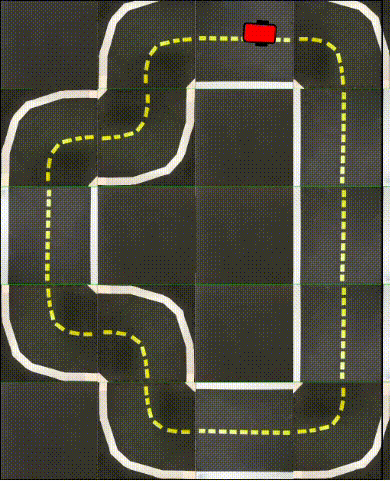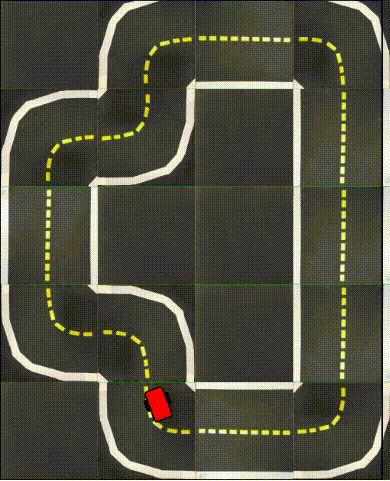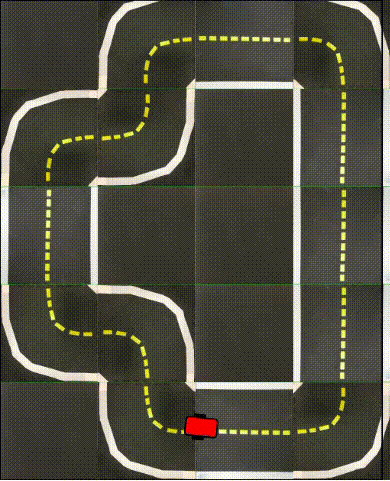
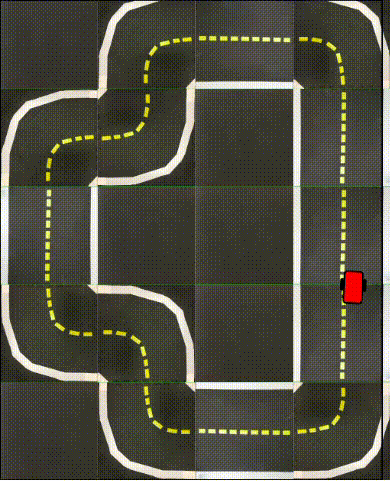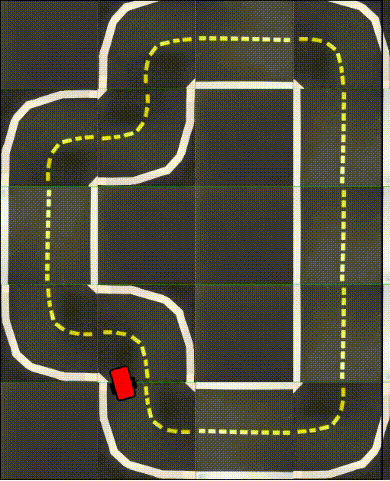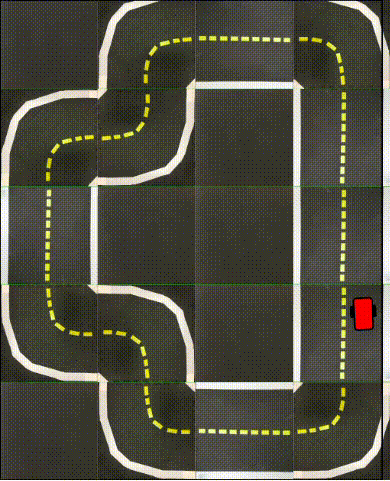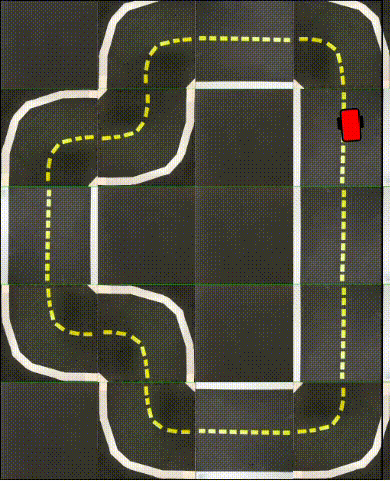
Real World

Finally, we are ready for real world experiments! We deploy the trained model from the best performing seed of the Simple ICRL experiments trained on the small loop in simulation. The real-world Duckietown map was built to mimic the small loop environment from simulation.

Though Sim2Real presents a significant hurdle, we can see that the policy has effectively transferred enough to make a few successful turns around the real-world loop. This is an encouraging result given that no specific Sim2Real procedures were performed to improve the robustness of the policy to the distribution shift from simulator to real-world.

Conclusion

In this work, we addressed the lane-following problem in autonomous driving using an inverse constrained RL approach. By learning the constraints of lane following as a residual component of the reward function using expert trajectories, Simple ICRL demonstrated a clear advantage over traditional RL and IRL models.

Our results showed that Simple ICRL achieves a balance across key metrics - deviation heading, distance traveled, and time spent in lane — outperforming RL models that rely entirely on the reward function or the IRL model that relies entirely on the expert trajectories. The model not only generalizes well in simulations but also transfers with some success to a real Duckiebot.

Notably, Simple ICRL is able to capture more complex behaviors, such as lane adherence, without needing a human to balance objectives manually in the reward function. This highlights the usefulness of incorporating expert trajectories to refine reward functions, offering a practical and computationally efficient solution to challenges in autonomous driving.